Алгоритмы и структуры данных

Сложность

Когда мы говорим об измерении сложности алгоритмов, мы подразумеваем анализ времени, которое потребуется для обработки очень большого набора данных. Такой анализ называют асимптотическим.

Порядок роста

Порядок роста описывает то, как сложность алгоритма растет с увеличением размера

входных данных. Чаще всего он представлен в виде O-нотации (от нем. «Ordnung»— порядок) : O(f(x)), где f(x) — формула, выражающая сложность алгоритма. В формуле может присутствовать переменная n, представляющая размер входных данных.

1. Константный — O(1)

Порядок роста O(1) означает, что вычислительная сложность алгоритма не зависит от размера входных данных. Следует помнить, однако, что единица в формуле не значит, что алгоритм выполняется за одну операцию или требует очень мало времени. Он может потребовать и микросекунду, и год. Важно то, что это время не зависит от входных данных.

public int GetCount(int[] items)
{
    return items.Length;
}

2. Линейный — O(n)

Порядок роста O(n) означает, что сложность алгоритма линейно растет с увеличением входного массива. Если линейный алгоритм обрабатывает один элемент пять миллисекунд, то мы можем ожидать, что тысячу элементов он обработает за пять секунд.

Такие алгоритмы легко узнать по наличию цикла по каждому элементу входного массива.

public long GetSum(int[] items)
{
    long sum = 0;
    foreach (int i in items)
    {
        sum += i;
    }

    return sum;
}

3. Логарифмический — O( log n)

Порядок роста O( log n) означает, что время выполнения алгоритма растет логарифмически с увеличением размера входного массива. (Прим. пер.: в анализе алгоритмов по умолчанию используется логарифм по основанию 2). Большинство алгоритмов, работающих по принципу «деления пополам», имеют логарифмическую сложность. Метод Contains бинарного дерева поиска (binary search tree) также имеет порядок роста O(log n).

4. Линеарифметический — O(n·log n)

Линеарифметический (или линейно-логарифмический) алгоритм имеет порядок роста O(n·log n). Некоторые алгоритмы типа «разделяй и властвуй» попадают в эту категорию. Примеры - сортировка слиянием и быстрая сортировка.

5. Квадратичный — O(n 2)

Время работы алгоритма с порядком роста O(n 2) зависит от квадрата размера входного массива. Несмотря на то, что такой ситуации иногда не избежать, квадратичная сложность — повод пересмотреть используемые алгоритмы или структуры данных. Проблема в том, что они плохо масштабируются.

function notSoSimpleCalculate(array) {
  for (let i = 0; i < array.length; i++) {
        for (let j = 0; j < array.length; j++) {
          array[i] = array[i] + array[j];
        }
  }
  return array;
}

Структуры данных и их сложность

1. Массив Массив — это простейшая и наиболее распространенная структура данных. Другие структуры данных, например, стеки и очереди, производны от массивов. Каждому элементу данных присваивается положительное числовое значение, именуемое индексом и соответствующее положению этого элемента в массиве. В большинстве языков программирования элементы в массиве нумеруются с 0. Существуют массивы двух типов:

• Одномерные

• Многомерные (массивы, в которые вложены другие массивы)

Первые имеют один индекс, вторые – два. Пусть одномерный массив называется A, тогда для получения доступа к его i-ому элементу потребуется указать название массива и номер требуемого элемента: A[i]. Когда A – матрица, то она представляема в виде таблицы, доступ к элементам которой осуществляется по имени массива, а также номерам строки и столбца, на пересечении которых расположен элемент: A[i, j], где i – номер строки, j – номер столбца.

2. Стек

Стек характерен тем, что получить доступ к его элементом можно лишь с одного конца, называемого вершиной стека, иначе говоря: стек – структура данных, функционирующая по принципу LIFO (last in — first out, «последним пришёл — первым вышел»). Изобразить эту структуру данных лучше в виде вертикального списка, например, стопки каких-либо вещей, где чтобы воспользоваться одной из них нужно поднять все те вещи, что лежат выше нее, а положить предмет можно лишь на вверх стопки.

Один из самых известных случаев, когда используется стек – хранение состояния программы и использование операции “Отмена”.

3. Очередь Очередь, как и стек — это линейная структура данных, элементы в которой хранятся в последовательном порядке. Единственное существенное отличие между стеком и очередью заключается в том, что в очереди вместо LIFO действует принцип FIFO (Первым пришел — первым вышел). Строго говоря, очередь – это список, добавление элементов в который допустимо, лишь в его конец, а их извлечение производиться с другой стороны, называемой началом списка.

4 . Дек

Дек (deque — double ended queue, «двухсторонняя очередь») – стек с двумя концами. Дек можно определять не только как двухстороннюю очередь, но и как стек, имеющий два конца. Это означает, что данный вид списка позволяет добавлять элементы в начало и в конец, и то же самое справедливо для операции извлечения.

Эта структура одновременно работает по двум способам организации данных: FIFO и LIFO. Поэтому ее допустимо отнести к отдельной программной единице, полученной в результате суммирования двух предыдущих видов списка.

5. Список

Список – абстрактный тип данных, реализующий упорядоченный набор значений. Списки отличаются от массивов тем, что доступ к их элементам осуществляется последовательно, в то время как массивы – структура данных произвольного доступа.

Список (связный список) – это структура данных, представляющая собой конечное множество упорядоченных элементов, связанных друг с другом посредствам указателей. Каждый элемент структуры содержит поле с какой-либо информацией, а также указатель на следующий элемент. В отличие от массива, к элементам списка нет произвольного доступа.

В односвязном списке, приведенным выше, начальным элементом является Head list (голова списка [произвольное наименование]), а все остальное называется хвостом. Хвост списка составляют элементы, разделенные на две части: информационную (поле info) и указательную (поле next). В последнем элементе вместо указателя, содержится признак конца списка – null.

При помощи связных списков реализуются файловые системы, хеш-таблицы и списки смежности.

Когда кроме указателя на следующий элемент есть указатель и на предыдущий, то такой список называется двусвязным.

Возможность двигаться как вперед, так и назад полезна для выполнения некоторых операций, но дополнительные указатели требуют задействования большего количества памяти, чем таковой необходимо в эквивалентном односвязном списке.

6. Граф

Граф – совокупность точек, соединенных линиями. Точки называются вершинами (узлами), а линии – ребрами (дугами).

Как показано на рисунке различают два основных вида графов: ориентированные и неориентированные. В первых ребра являются направленными, т. е. существует только одно доступное направление между двумя связными вершинами, например из вершины 1 можно пройти в вершину 2, но не наоборот. В неориентированном связном графе из каждой вершины можно пройти в каждую и обратно. Частный случай двух этих видов – смешанный граф. Он характерен наличием как ориентированных, так и неориентированных ребер.

Степень входа вершины – количество входящих в нее ребер, степень выхода – количество исходящих ребер.

Ребра графа необязательно должны быть прямыми, а вершины обозначаться именно цифрами, так как показано на рисунке. К тому же встречаются такие графы, ребрам которых поставлено в соответствие конкретное значение, они именуются взвешенными графами, а это значение – весом ребра. Когда у ребра оба конца совпадают, т. е. ребро выходит из вершины F и входит в нее, то такое ребро называется петлей.

Графы широко используются в структурах, созданных человеком, например в компьютерных и транспортных сетях, web-технологиях. Специальные способы представления позволяют использовать граф в информатике (в вычислительных машинах). Самые известные из них: «Матрица смежности», «Матрица инцидентности», «Список смежности», «Список рёбер». Два первых, как понятно из названия, для репрезентации графа используют матрицу, а два последних – список.

7.Дерево

Дерево как математический объект это абстракция из соименных единиц, встречающихся в природе. Схожесть структуры естественных деревьев с графами определенного вида говорит о допущении установления аналогии между ними. А именно со связанными и вместе с этим ациклическими (не имеющими циклов) графами. Последние по своему строению действительно напоминают деревья, но в чем то и имеются различия, например, принято изображать математические деревья с корнем расположенным вверху, т. е. все ветви «растут» сверху вниз. Известно же, что в природе это совсем не так.

Поскольку дерево это по своей сути граф, у него с последним многие определения совпадают, либо интуитивно схожи. Так корневой узел (вершина 6) в структуре дерева – это единственная вершина (узел), характерная отсутствием предков, т. е. такая, что на нее не ссылается ни какая другая вершина, а из самого корневого узла можно дойти до любой из имеющихся вершин дерева, что следует из свойства связности данной структуры. Узлы, не ссылающиеся ни на какие другие узлы, иначе говоря, ни имеющие потомков называются листьями (2, 3, 9), либо терминальными узлами. Элементы, расположенные между корневым узлом и листьями – промежуточные узлы (1, 1, 7, 8). Каждый узел дерева имеет только одного предка, или если он корневой, то не имеет ни одного.

С деревом можно выполнять многие операции, например, находить элементы, удалять элементы и поддеревья, вставлять поддеревья, находить корневые узлы для некоторых вершин и др. Одной из важнейших операций является обход дерева. Выделяются несколько методов обхода. Наиболее популярные из них: симметричный, прямой и обратный обход. При прямом обходе узлы-предки посещаются прежде своих потомков, а в обратном обходе, соответственно, обратная ситуация. В симметричном обходе поочередно просматриваются поддеревья главного дерева.

8. Хеш-таблицы

Хеш-таблица — это структура данных для хранения пар ключей и их значений. По сути она представляет собой массив, где местоположение элемента зависит от значения самого элемента. Связь между значением элемента и его позицией в хеш-таблице задает хеш-функция. Важное свойство хеш-таблицы: поиск, вставка и удаление элементов из таблицы выполняются за фиксированное время, то есть О(1), то есть они нужны тогда, когда максимально важна скорость этих операций.

Хеш-функция — это функция, которая принимает в качестве аргумента какой-то элемент (который нужно вставить в хеш-таблицу), а в результате выдает позицию заданного элемента в хеш-таблицы.

Хеш-функция принимает ключ на вход и вычисляет индекс массива, исходя из внутренних свойств этого ключа.

Сначала вам нужно использовать хеш-функцию, чтобы определить, где в хеш-таблице хранится данный ключ. Затем нужно будет использовать ту же самую хеш-функцию, чтобы определить, где в хеш-таблице искать данный ключ. По этой причине важно, чтобы хеш-функция вела себя последовательно и выводила один и тот же индекс для одинаковых входных данных.

Ситуация, когда для разных ключей получается одно и то же хеш-значение, называется коллизией или столкновением.

Двумя распространенными методами борьбы с коллизиями являются линейное зондирование и метод цепочек.

Линейное зондирование заключается в поиске первой пустой ячейки после той, на которую указала хеш-функция.

При методе цепочек, каждая ячейка хеш-таблицы — это список значений. При возникновении коллизии, новое значение просто добавляется в список в ту же ячейку таблицы.

Алгоритмы

1. Сортировка пузырьком

Данный алгоритм сортировки известен в первую очередь за счёт своей простоты, однако при этом он имеет одну из наиболее низких скоростей выполнения.

Алгоритм:

• сравнить два числа;

• если число слева больше, то поменять их местами;

• перейти на одну позицию вправо.

После прохождения по всей цепочки с выполнением данных шагов мы обнаружим, что наибольшее число оказалось в конце нашего ряда чисел. Далее выполняется точно такой же проход по цепочке с выполнением вышеописанных шагов. Но в этот раз мы не будем включать последний элемент списка, так как он самый большой и уже стоит на последнем месте, как и должен. Опять, же мы получим последний элемент в конце нашего ряда рассматриваемых чисел. Соответственно, уже два наибольших числа будут стоять на своих местах. И опять запускается проход по цепочке за исключением элементов, которые уже на своих местах, до тех пор, пока все элементы не будут стоять в необходимом порядке.

Пузырьковая сортировка весьма и весьма медленная, с временной сложностью O(N²), так как мы имеем вложенные циклы. Внешний проход по элементам выполняется за N раз, внутренний — тоже N раз, и в итоге мы получаем N*N, N² итераций.

Реализация:

public static void  bubbleSort(int[] array) {
       for(int i = array.length -1; i > 1; i--) {
         for (int j = 0; j < i; j++) { //
             if (array[j] > array[j+1]) {
                 int temp = array[j];
                 array[j] = array[j+1];
                 array[j+1] = temp;
             }
}

2. Сортировка методом выбора

Данный алгоритм имеет схожесть с пузырьковой сортировкой, но работает он несколько быстрее. Суть алгоритма заключается в последовательном переборе всех чисел и выборе наименьшего элемента, который мы возьмём и поменяем местами с крайним элементом слева (0 элементом). Тут у нас получается ситуация, схожая с пузырьковой сортировкой, но в данном случае отсортированным элементом у нас будет наименьший. Поэтому, следующий проход по элементам будет начинаться с элемента под индексом 1. Опять же, данные проходы будет повторяться до тех пор, пока все элементы не будут отсортированы.

Реализация:

public static void sortBySelect(int[] array) {

       for (int i = 0; i < array.length-1; i++) { // внешний обычный  цикл
           int min = i;

           for (int j = i + 1; j < array.length; j++) { // обычный цикл, но с отчетом с сортированных чисел
               if (array[j] < array[min]) {
                   min = j;
               }
           }
           int temp = array[i];     // вставка отссортиованного числа, в положеную ему ячейку
           array[i] = array[min];
           array[min] = temp;
       }
   }
}

3. Сортировка методом вставки

Данный алгоритм заключается в выставлении маркера, слева от которого элементы будут уже частично отсортированы между собой. На каждом шаге алгоритма будет выбираться один из элементов и помещаться на нужную позицию в уже отсортированной последовательности. Таким образом, отсортированная часть будет увеличиваться до тех пор, пока не будут просмотрены все элементы.

Реализация:

 public static void insertionSort(int[] array) {

       for (int i = 1; i < array.length; i++) { // i - разделяющий маркер
           int temp = array[i]; // делаем копию помеченного элемента
           int j = i;
           while (j     > 0 && array[j - 1] >= temp) { // пока не будет найден меньший элемент
               array[j] = array[j - 1]; // сдвигаем элементы вправо
               --j;
           }
           array[j] = temp;   // вставляем отмеченный элемент, в положеное ему место
       }
   }

4. Быстрая сортировка

Данную сортировку ещё называют сортировкой Хоара. Это один из самых популярных алгоритмов, и поэтому на него стоит обратить особое внимание. Суть данного алгоритма заключается в том, что в списке с элементами выбирается опорный элемент — по сути любой элемент, относительно которого нужно отсортировать остальные значения. Значения меньше его — слева, значения больше — справа. Далее у правой и левой части также выбирается по опорному элементу и происходит то же самое: сортируются значения относительно этих элементов, потом у образовавшихся частей выбираются опорные элементы — и так до тех пор, пока мы не получим отсортированный ряд.

Реализация:

public static void fastSort(int[] array) {
       recursionFastSort(array, 0, array.length - 1);
   }

   public static void recursionFastSort(int[] array, int min, int max) {
       if (array.length == 0)// условие выхода из рекурсии,  если длина массива равна 0
           return;

       if (min >= max) //выходим, так как нечего уже делить
           return;

       int middle = min + (max - min) / 2;  // выбираем середину
       int middleElement = array[middle];

       int i = min, j = max;
       while (i <= j) {  // относительно элемента middle определяемменьшие элементы слева, большие справа
           while (array[i] < middleElement) {
               i++;
           }
           while (array[j] > middleElement) {
               j--;
           }

           if (i <= j) {      //меняем местами
               int temp = array[i];
               array[i] = array[j];
               array[j] = temp;
               i++;
               j--;
           }
       }

       if (min < j) // запускаем рекурсию с элементами меньшими чем middle
           recursionFastSort(array, min, j);

       if (max > i)// запускаем рекурсию с элементами большими чем middle
           recursionFastSort(array, i, max);
   }

5. Сортировка слиянием

Она относится к одному из видов алгоритмов, работающих по принципу «разделяй и властвуй»: в них мы в первую очередь делим задачи на минимальные части (также представителем таких алгоритмов является быстрая сортировка).

Разделяй:

Массив разбивается на две части примерно одинакового размера, каждая из этих двух частей делится еще на две, и так далее, пока не останутся наименьшие неделимые части. Наименьшие неделимые части — это когда в каждом массиве есть по одному элементу, а значит, такой массив автоматически считается отсортированным.

Властвуй:

Берутся два получившиеся упорядоченных массива и сливаются в один. При этом наименьший из первых элементов двух массивов записывается в результирующий массив, и эта операция повторяется, пока не закончатся элементы в этих двух массивах.

Реализация:

public static int[] mergeSort(int[] array1) {
       int[] sortArr = Arrays.copyOf(array1, array1.length);// массив для сортировки
       int[] bufferArr = new int[array1.length];// буферный массив
       return recurtionMergeSort(sortArr, bufferArr, 0, array1.length);
   }
   public static int[] recurtionMergeSort(int[] sortArr, int[] bufferArr,
                                          int startIndex, int endIndex) {
       if (startIndex >= endIndex - 1) {// выход из массива, когда в рассматриваемом промежутке массива, только один элемент
           return sortArr;
       }
       // запускаем рекурсию, чтобы получить два отсортированных массива:
       int middle = startIndex + (endIndex - startIndex) / 2;
       int[] firstSortArr = recurtionMergeSort(sortArr, bufferArr, startIndex, middle);
       int[] secondSortArr = recurtionMergeSort(sortArr, bufferArr, middle, endIndex);

       // Слияние отсортированных массивов:
       int firstIndex = startIndex;
       int secondIndex = middle;
       int destIndex = startIndex;
       int[] result = firstSortArr == sortArr ? bufferArr : sortArr;
       while (firstIndex < middle && secondIndex < endIndex) {
           result[destIndex++] = firstSortArr[firstIndex] < secondSortArr[secondIndex]
                   ? firstSortArr[firstIndex++] : secondSortArr[secondIndex++];
       }
       while (firstIndex < middle) {
           result[destIndex++] = firstSortArr[firstIndex++];
       }
       while (secondIndex < endIndex) {
           result[destIndex++] = secondSortArr[secondIndex++];
       }
       return result;
   }
Алгоритмы поиска в графах

Одна из основных операций, которые выполняются с графами, — это определение всех вершин, достижимых от заданной вершины. Существует два основных способа обхода графов: обход в глубину и обход в ширину, которые мы и рассмотрим. Оба способа обеспечат перебор всех связных вершин.

Обход в глубину

Это один из наиболее распространенных методов обхода графа. Данная стратегия поиска в глубину состоит в том, чтобы идти «вглубь» графа насколько это возможно, а достигнув тупика, возвращаться к ближайшей вершине, у которой есть смежные ранее не посещенные вершины. Этот алгоритм хранит в стеке информацию о том, куда следует вернуться при достижении “тупика”. Правила обхода в глубину:

1. Посетить смежную, ранее не посещенную вершину, пометить её и занести в стек.

2. Перейти на данную вершину.

3. Повторить этап 1.

4. Если выполнение пункта 1 невозможно, вернуться к предыдущей вершины и попытаться повторить правило 1. Если это невозможно — вернуться к вершине до нее, и так далее, пока не найдем вершину, с которой можно продолжить обход.

5. Продолжать до тех пор, пока все вершины не окажутся в стеке.

Обход в ширину

Данный алгоритм, как и обход в глубину, является одним наиболее простых и базовых методов обхода графа. Его суть в том, что у нас есть некоторая текущая вершина, с которой мы все смежные, непройденные вершины, заносим в очередь и выбираем следующий элемент (который хранится первым в очереди), чтобы его сделать текущим…Если разбить данный алгоритм на этапы, можно выделить следующие правила:

1. Посетить следующую, ранее не посещенную вершину, смежную с текущей вершиной, пометить её заранее и занести в очередь.

2. Если выполнение правила #1 невозможно — извлечь вершину из очереди и сделать её текущей вершиной.

3. Если правило #1 и #2 невозможно, обход закончен, а все вершины пройдены (если граф у нас связный).

Алгоритм Дейкстры

Как говорилось ранее, графы могут быть направленными и ненаправленными. И как вы помните, они ещё могут быть взвешенными. Одной из самых распространённых задач, связанной со взвешенными графами, является задача выбора кратчайшего пути между двумя вершинами. Для решения данной задачи мы и используем алгоритм Дейкстры. Этапы алгоритма Дейкстры:

• Этап 1: поиск узла, переход к которому будет составлять наименьшую стоимость. Вы стоите в самом начале и думаете, куда направиться: к узлу А или к узлу В. Сколько времени понадобится, чтобы добраться до каждого из этих узлов?

• Этап 2: вычисление, сколько времени нужно, чтобы добраться до всех ещё не затронутых алгоритмом соседей В при переходе по ребру из В. Если же это новое время окажется меньше старого, путь через ребро B и станет новым кратчайшим путём для этой вершины.

• Этап 3: помечаем вершину B как пройденную.

• Этап 4: перейти к этапу 1.

Цикл этих этапов мы будем повторять до тех пор, пока все вершины не будут пройдены.

Алгоритмы поиска Последовательный (линейный) поиск – это простейший вид поиска заданного элемента на некотором множестве, осуществляемый путем последовательного сравнения очередного рассматриваемого значения с искомым до тех пор, пока эти значения не совпадут.

Идея этого метода заключается в следующем. Множество элементов просматривается последовательно в некотором порядке, гарантирующем, что будут просмотрены все элементы множества (например, слева направо). Если в ходе просмотра множества будет найден искомый элемент, просмотр прекращается с положительным результатом; если же будет просмотрено все множество, а элемент не будет найден, алгоритм должен выдать отрицательный результат.

Алгоритм последовательного поиска

Шаг 1. Полагаем, что значение переменной цикла i=0.

Шаг 2. Если значение элемента массива x[i] равно значению ключа key, то возвращаем значение, равное номеру искомого элемента, и алгоритм завершает работу. В противном случае значение переменной цикла увеличивается на единицу i=i+1.

Шаг 3. Если i<k, где k – число элементов массива x, то выполняется Шаг 2, в противном случае – работа алгоритма завершена и возвращается значение равное -1.

При наличии в массиве нескольких элементов со значением key данный алгоритм находит только первый из них (с наименьшим индексом).

Недостатком рассматриваемого алгоритма поиска является то, что в худшем случае осуществляется просмотр всего массива. Поэтому данный алгоритм используется, если множество содержит небольшое количество элементов.

Достоинства последовательного поиска заключаются в том, что он прост в реализации, не требует сортировки значений множества, дополнительной памяти и дополнительного анализа функций. Следовательно, может работать в потоковом режиме при непосредственном получении данных из любого источника.

Бинарный (двоичный, дихотомический) поиск – это поиск заданного элемента на упорядоченном множестве, осуществляемый путем неоднократного деления этого множества на две части таким образом, что искомый элемент попадает в одну из этих частей. Поиск заканчивается при совпадении искомого элемента с элементом, который является границей между частями множества или при отсутствии искомого элемента.

Бинарный поиск применяется к отсортированным множествам и заключается в последовательном разбиении множества пополам и поиска элемента только в одной половине на каждой итерации.

Таким образом, идея этого метода заключается в следующем. Поиск нужного значения среди элементов упорядоченного массива (по возрастанию или по убыванию) начинается с определения значения центрального элемента этого массива. Значение данного элемента сравнивается с искомым значением и в зависимости от результатов сравнения предпринимаются определенные действия. Если искомое и центральное значения оказываются равны, то поиск завершается успешно. Если искомое значение меньше центрального или больше, то формируется массив, состоящий из элементов, находящихся слева или справа от центрального соответственно. Затем поиск повторяется в новом массиве.

Алгоритм бинарного поиска

Шаг 1. Определить номер среднего элемента массива middle = (high + low) / 2.

Шаг 2. Если значение среднего элемента массива равно искомому, то возвращаем значение, равное номеру искомого элемента, и алгоритм завершает работу.

Шаг 3. Если искомое значение больше значения среднего элемента, то возьмем в качестве массива все элементы справа от среднего, иначе возьмем в качестве массива все элементы слева от среднего (в зависимости от характера упорядоченности). Перейдем к Шагу 1.

В массиве может встречаться несколько элементов со значениями, равными ключу. Данный алгоритм находит первый совпавший с ключом элемент, который в порядке следования в массиве может быть ни первым, ни последним среди равных ключу. Например, в массиве чисел 1, 5, 5, 5, 5, 5, 5, 7, 8 с ключом key =5 совпадет элемент с порядковым номером 4, который не относится ни к первому, ни к последнему.

Поиск

Сортировка

Структуры данных

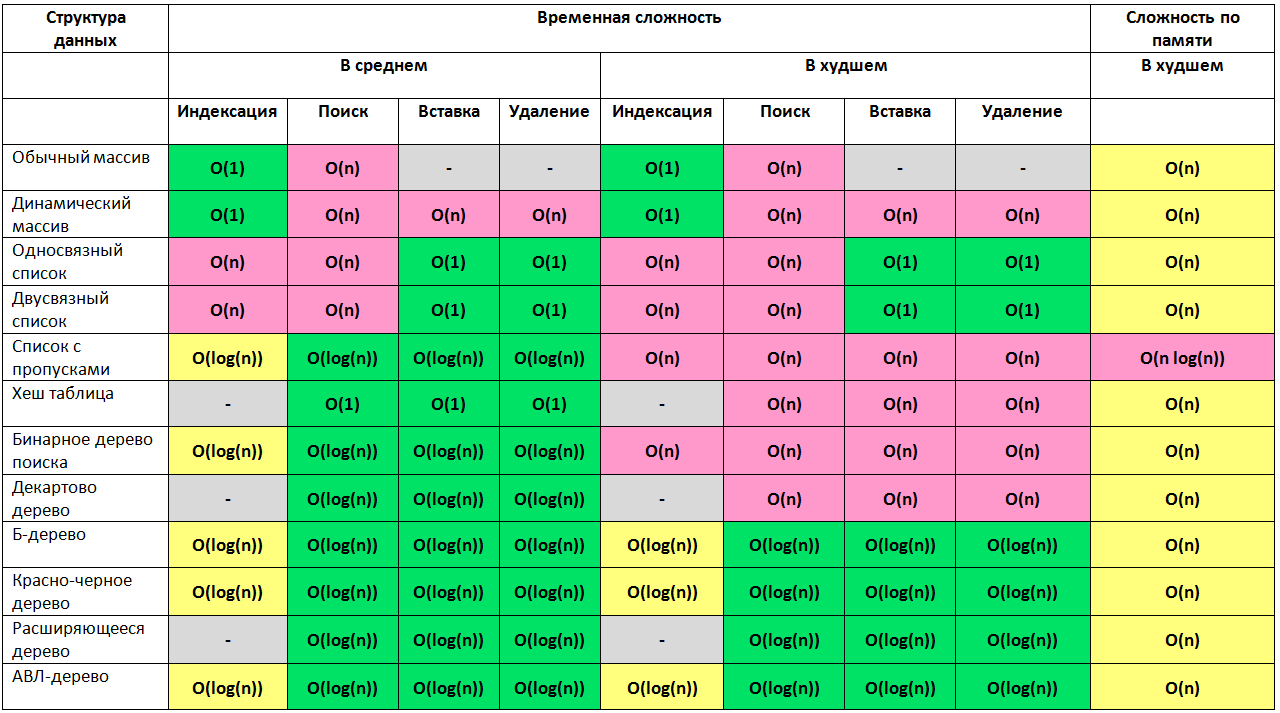
Кучи

Представление графов

Пусть дан граф с |V| вершинами и |E| ребрами, тогда

Нотация асимптотического роста

1. (О — большое) — верхняя граница, в то время как (Омега — большое) — нижняя граница. Тета требует как (О — большое), так и (Омега — большое), поэтому она является точной оценкой (она должна быть ограничена как сверху, так и снизу). К примеру, алгоритм требующий Ω (n logn) требует не менее n logn времени, но верхняя граница не известна. Алгоритм требующий Θ (n logn) предпочтительнее потому, что он требует не менее n logn (Ω (n logn)) и не более чем n logn (O(n logn)).

2. f(x)=Θ(g(n)) означает, что f растет так же как и g когда n стремится к бесконечности. Другими словами, скорость роста f(x) асимптотически пропорциональна скорости роста g(n).

3. f(x)=O(g(n)). Здесь темпы роста не быстрее, чем g (n). O большое является наиболее полезной, поскольку представляет наихудший случай.

Короче говоря, если алгоритм имеет сложность __ тогда его эффективность __

График роста O — большое